Important Questions for Class 10 Maths Chapter 9 Some Applications of Trigonometry with solutions includes all the important topics with detailed explanation that aims to help students to score more marks in Board Exams 2020. Students who are preparing for their Class 10 exams must go through Important Questions for Class 10 Math Chapter 9 Some Applications of Trigonometry.
- Applications Of Trigonometry Worksheet Answers
- Applications Of Trigonometry Class 10 Answers
- Applications Of Trigonometry Word Problems Worksheet Answers
- Applications Of Right Triangle Trigonometry Worksheet Answers

- NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry provides comprehensive solutions for all the questions in the NCERT textbook. To excel in the board examinations, NCERT solutions will increase the level of confidence among the students, as the concepts are clearly explained and structured.
- Trigonometry (10th Edition) answers to Chapter 7 - Applications of Trigonometry and Vectors - Section 7.5 Applications of Vectors - 7.5 Exercises - Page 337 24 including work step by step written by community members like you. Textbook Authors: Lial, Margaret L.; Hornsby, John; Schneider, David I.; Daniels, Callie, ISBN-10:, ISBN-13: 978-0-32167-177-6.
- Trigonometric formulae are useful for solving problems in two dimensions. However, in the real world all objects are three dimensional, so it is important that we extend the application of the area, sine and cosine formulae to three dimensional situations. Drawing a three dimensional diagram is a crucial step in finding the solution to a problem.
(BE) is a diameter of semi-circle (BAE). (O) is the centre and therefore bisects (BE). [begin{array}{rll} OA &= OE = OB &text{ (equal radii)} therefore O hat{A} E &= theta &text{ (opp. } angle text{'s of equal sides)} therefore A hat{O} C &= theta + theta &text{ (ext. } angle text{ of } triangle OAE text{ = sum int. opp.)} &=2theta &end{array}]
Or
[begin{array}{rll} A hat{O} C &= 2theta & (angle text{ at centre } = 2 angle text{ at circum. })end{array}]Related Pages
Trigonometry Word Problems
Lessons On Trigonometry
Inverse trigonometry
Trigonometry Worksheets
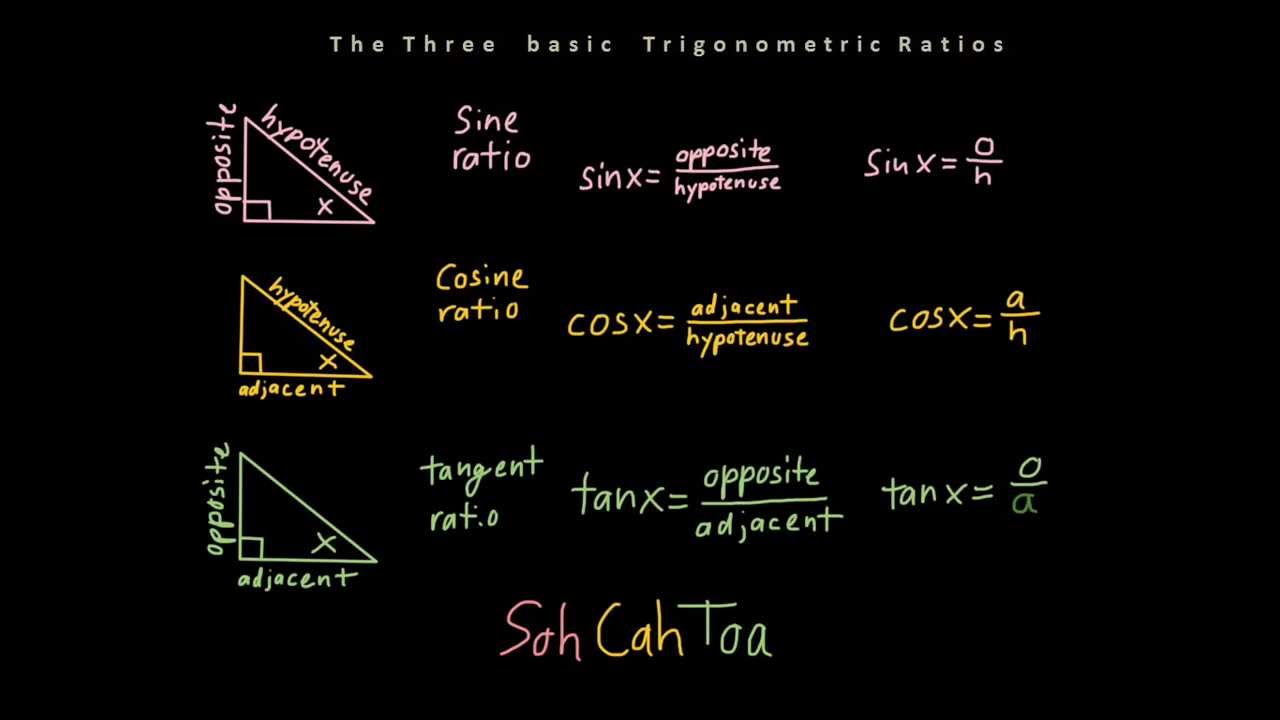
Hints On Solving Word Problems Or Applications Of Trigonometry:
- If no diagram is given, draw one yourself.
- Mark the right angles in the diagram.
- Show the sizes of the other angles and the lengths of any lines that are known
- Mark the angles or sides you have to calculate.
- Consider whether you need to create right triangles by drawing extra lines. For example, divide an isosceles triangle into two congruent right triangles.
- Decide whether you will need Pythagorean theorem, sine, cosine or tangent.
- Check that your answer is reasonable. For example, the hypotenuse is the longest side in a right triangle.
Example:
A ladder 5 m long, leaning against a vertical wall makes an angle of 65˚ with the ground.
a) How high on the wall does the ladder reach?
b) How far is the foot of the ladder from the wall?
c) What angle does the ladder make with the wall?
Solution:
a) The height that the ladder reach is PQ

PQ = sin 65˚ × 5 = 4.53 m
b) The distance of the foot of the ladder from the wall is RQ.

RQ = cos 65˚ × 5 = 2.11 m
c) The angle that the ladder makes with the wall is angle P
Videos
The following videos shows more examples of solving application of trigonometry word problems.
Example 1: Suppose that a 10 meter ladder is leaning against a building such that the angle of elevation from ground to the building is 62 degrees. Find the distance of the foot of the ladder from the wall. Also, find the distance from the ground to the top of the ladder.
Example 2: Suppose that from atop a 100m vertical cliff a ship is spotted at an angle of depression of 12 degrees. How far is the ship from the base of the cliff? Also, find the distance from the top of the cliff to the ship.
- Show Video Lesson
Trigonometry Word Problem
How to Find The Height of a Building using trigonometry?
Example:
A hiker is hiking up a 12 degrees slope. If he hikes at a constant rate of 3 mph, how much altitude does he gain in 5 hours of hiking?
- Show Video Lesson
Example:
A balloon is hovering 800 ft above a lake. The balloon is observed by the crew of a boat as they look upwards at an angle of 20 degrees. Twenty-five seconds later, the crew has tolook at angle of 65 degrees to see the balloon. How fast was the boat traveling?
Trigonometry word problems (part 1)
Navigation Problem: The first part of a problem when the captain of a ship goes off track.

- Show Video Lesson
Applications Of Trigonometry Worksheet Answers
Trigonometry word problems (part 2)
The second part of the problem of the off-track ship captain.
Applications Of Trigonometry Class 10 Answers
Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.
Applications Of Trigonometry Word Problems Worksheet Answers
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.